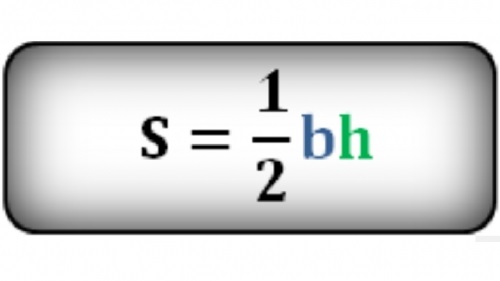Каждый ученик, отлынивающий от занятий, не раз слышал от взрослых, что знания, полученные на уроках, не раз пригодятся во взрослой жизни, но верилось в это с трудом. Тем не менее, реальность зачастую подводит нас к тому, что надо воспользоваться самими элементарными знаниями химии, физики или геометрии, например, найти площадь равнобедренного треугольника…
Равнобедренный треугольник
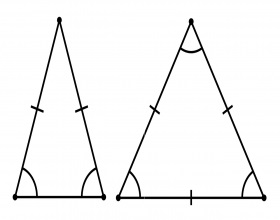
Равнобедренным треугольником называют геометрическую фигуру с двумя идентичными сторонами (равными по длине). Эти две одинаковые стороны называются боковыми. Оставшаяся третья сторона с отличной длиной называется основанием.
Существует также понятие правильного треугольника, в котором и боковые стороны, и основание имеют одинаковую длину. Правильный треугольник тоже можно назвать равнобедренным, за тем исключением, что вместо привычных двух одинаковых сторон, у него их – три. Обратное утверждение этого факта будет считаться неверным.
Свойства
Чтобы найти площадь равнобедренного треугольника, необходимо знать его основные свойства.
Существует три свойства, необходимые для вычислительных действий:
- Углы, которые находятся напротив равных сторон геометрической фигуры, также равны по отношению друг к другу. Биссектрисы, высоты и медианы, которые будут проведены из этих углов, тоже будут равными.
- Если провести биссектрису, высоту, медианы и начертить срединный перпендикуляр, проходящий по центральной точке основания, то они совпадут между собой. На этой линии будут лежать центры описанной и вписанной в треугольник окружностей.
- Углы по обеим сторонам основания идентичны друг другу.
Как рассчитать площадь равнобедренного треугольника
Найдите площадь равнобедренного треугольника, воспользовавшись общеизвестной формулой.
Для этого необходимо узнать, чему равно произведение половины основания и высоты.
Но как быть, если высота или длина основания неизвестны? Рассмотрим несколько примеров вычисления неизвестных составляющих для нахождения площади равнобедренного треугольника.
Если вам известна длина основания и длина боковой стороны, можно воспользоваться теоремой Пифагора (а2+b2=с2), чтобы найти высоту. Поскольку боковая сторона является гипотенузой, а ½ основания – катетом, можно запросто узнать необходимое значение.
Если вы знаете, чему равна длина основания и сколько градусов составляет угол между основанием и боковой стороной, этого вполне достаточно, чтобы найти площадь равнобедренного треугольника. Из соотношения сторон по формуле h=c*ctg(B)/2 необходимо найти высоту, поделив сторону с на две части. После этого у вас будут все необходимые значения.
Если вам дана высота и угол между основанием и одной из боковых сторон, сперва следует найти высоту из соотношения двух сторон фигуры по формуле c=h*tg(B)*2. Полученный результат будет являться половиной основания, следовательно, его нужно удвоить. После этого можно узнать площадь по формуле, приведенной выше.
Как видите, узнать площадь равнобедренного треугольника не составит труда, даже если у вас на руках присутствует минимальное количество информации. Не все школьные знания могут пригодиться в жизни, но в данном случае быстрые вычисления помогут вам решить вопросы организации пространства или расхода материалов (строительство, творчество и т.д.).
